First, write down a list of your daily activities that you typically do on a weekday. For instance, you might get out of bed, take a shower, get dressed, eat breakfast, dry your hair, brush your teeth, etc. Make sure to break down your list so you have a minimum of 10 activities.
7.1.1 [5] <7.2> Now consider which of these activities is already exploiting some form of parallelism (e.g., brushing multiple teeth at the same time, versus one at a time, carrying one book at a time to school, versus loading them all into your backpack and then carry them “in parallel”). For each of your activities, discuss if they are already working in parallel, but if not, why they are not.
7.1.2 [5] <7.2> Next, consider which of the activities could be carried out concurrently (e.g., eating breakfast and listening to the news). For each of your activities, describe which other activity could be paired with this activity.
7.1.3 [5] <7.2> For 7.1.2, what could we change about current systems (e.g., showers, clothes, TVs, cars) so that we could perform more tasks in parallel?
7.1.4 [5] <7.2> Estimate how much shorter time it would take to carry out these activities if you tried to carry out as many tasks in parallel as possible.
Exercise 7.2
Many computer applications involve searching through a set of data and sorting the data. A number of efficient searching and sorting algorithms have been devised in order to reduce the runtime of these tedious tasks. In this problem we will consider how best to parallelize these tasks.
7.2.1 [10] <7.2> Consider the following binary search algorithm (a classic divide and conquer algorithm) that searches for a value X in an sorted Nelement array A and returns the index of matched entry:

Assume that you have Y cores on a multicore processor to run BinarySearch. Assuming that Y is much smaller than N, express the speedup factor you might expect to obtain for values of Y and N. Plot these on a graph.
7.2.2 [5] <7.2> Next, assume that Y is equal to N. How would this affect your conclusions in your previous answer? If you were tasked with obtaining the best speedup factor possible (i.e., strong scaling), explain how you might change this code to obtain it.
Exercise 7.3
Consider the following piece of C code:
for (j=2;j<1000;j++)
D[j] = D[j-1]+D[j-2];
The MIPS code corresponding to the above fragment is:
DADDIU r2,r2,999
loop: L.D f1, -16(f1)
L.D f2, -8(f1)
ADD.D f3, f1, f2
S.D f3, 0(r1)
DADDIU r1, r1, 8
BNE r1, r2, loop
Instructions have the following associated latencies (in cycles):

7.3.1 [10] <7.2> How many cycles does it take for all instructions in a single iteration of the above loop to execute?
7.3.2 [10] <7.2> When an instruction in a later iteration of a loop depends upon a data value produced in an earlier iteration of the same loop, we say that there is a loop carried dependence between iterations of the loop. Identify the loop carried dependences in the above code. Identify the dependent program variable and assemblylevel registers. You can ignore the loop induction variable j.
7.3.3 [10] <7.2> Loop unrolling was described in Chapter 4. Apply loop unrolling to this loop and then consider running this code on a 2node distributed memory message passing system. Assume that we are going to use message passing as described in Section 7.4, where we introduce a new operation send (x, y) that sends to node x the value y, and an operation receive( ) that waits for the value being sent to it. Assume that send operations take a cycle to issue (i.e., later instructions on the same node can proceed on the next cycle), but take 10 cycles be received on the receiving node. Receive instructions stall execution on the node where they are executed until they receive a message. Produce a schedule for the two nodes assuming an unroll factor of 4 for the loop body (i.e., the loop body will appear 4 times). Compute the number of cycles it will take for the loop to run on the message passing system.
7.3.4 [10] <7.2> The latency of the interconnect network plays a large role in the efficiency of message passing systems. How fast does the interconnect need to be in order to obtain any speedup from using the distributed system described in 7.3.3?
Exercise 7.4
Consider the following recursive mergesort algorithm (another classic divide and conquer algorithm). Mergesort was first described by John Von Neumann in 1945. The basic idea is to divide an unsorted list x of m elements into two sublists of about half the size of the original list. Repeat this operation on each sublist, and continue until we have lists of size 1 in length. Then starting with sublists of length 1, “merge” the two sublists into a single sorted list.
Mergesort(m)
var list left, right, result
if length(m) ≤ 1
return m
else
var middle = length(m) / 2
for each x in m up to middle
add x to left
for each x in m after middle
add x to right
left = Mergesort(left)
right = Mergesort(right)
result = Merge(left, right)
return result
The merge step is carried out by the following code:
Merge(left,right)
var list result
while length(left) > 0 and length(right) > 0
if first(left) ≤ first(right)
append first(left) to result
left = rest(left)
else
append first(right) to result
right = rest(right)
if length(left) > 0
append rest(left) to result
if length(right) > 0
append rest(right) to result
return result
7.4.1 [10] <7.2> Assume that you have Y cores on a multicore processor to run MergeSort. Assuming that Y is much smaller than length(m), express the speedup factor you might expect to obtain for values of Y and length(m). Plot these on a graph.
7.4.2 [10] <7.2> Next, assume that Y is equal to length(m). How would this affect your conclusions your previous answer? If you were tasked with obtaining the best speedup factor possible (i.e., strong scaling), explain how you might change this code to obtain it.
Exercise 7.5
You are trying to bake 3 blueberry pound cakes. Cake ingredients are as follows:
1 cup butter, softened
1 cup sugar
4 large eggs
1 teaspoon vanilla extract
1/2 teaspoon salt
1/4 teaspoon nutmeg
1 1/2 cups flour
1 cup blueberries
The recipe for a single cake is as follows:
Step 1: Preheat oven to 325°F (160°C). Grease and flour your cake pan.
Step 2: In large bowl, beat together with a mixer butter and sugar at medium speed until light and fluffy. Add eggs, vanilla, salt and nutmeg. Beat until thoroughly blended. Reduce mixer speed to low and add flour, 1/2 cup at a time, beating just until blended.
Step 3: Gently fold in blueberries. Spread evenly in prepared baking pan. Bake for 60 minutes.
7.5.1 [5] <7.2> Your job is to cook 3 cakes as efficiently as possible. Assuming that you only have one oven large enough to hold one cake, one large bowl, one cake pan, and one mixer, come up with a schedule to make three cakes as quickly as possible. Identify the bottlenecks in completing this task.
7.5.2 [5] <7.2> Assume now that you have three bowls, 3 cake pans and 3 mixers. How much faster is the process now that you have additional resources?
7.5.3 [5] <7.2> Assume now that you have two friends that will help you cook, and that you have a large oven that can accommodate all three cakes. How will this change the schedule you arrived at in 7.5.1 above?
7.5.4 [5] <7.2> Compare the cakemaking task to computing 3 iterations of a loop on a parallel computer. Identify datalevel parallelism and tasklevel parallelism in the cakemaking loop.
Exercise 7.6
Matrix multiplication plays an important role in a number of applications. Two matrices can only be multiplied if the number of columns of the first matrix is equal to the number of rows in the second. Let’s assume we have an m × n matrix A and we want to multiply it by an n × p matrix B. We can express their product as an m × p matrix denoted by AB (or A · B). If we assign C = AB, and ci,j denotes the entry in C at position (i, j), then

for each element i and j with 1 ≤ i ≤ m and 1 ≤ j ≤ p. Now we want to see if we can parallelize the computation of C. Assume that matrices are laid out in memory sequentially as follows: a1,1, a2,1, a3,1, a4,1, …, etc..
7.6.1 [10] <7.3> Assume that we are going to compute C on both a single core shared memory machine and a 4core sharedmemory machine. Compute the speedup we would expect to obtain on the 4core machine, ignoring any memory issues.
7.6.2 [10] <7.3> Repeat 7.6.1, assuming that updates to C incur a cache miss due to false sharing when consecutive elements are in a row (i.e., index i) are updated.
7.6.3 [10] <7.3> How would you fix the false sharing issue that can occur?
Exercise 7.7
Consider the following portions of two different programs running at the same time on four processors in a symmetric multicore processor (SMP). Assume that before this code is run, both x and y are 0.
Core 1: x = 2;
Core 2: y = 2;
Core 3: w = x + y + 1;
Core 4: z = x + y;
7.7.1 [10] <7.3> What are all the possible resulting values of w, x, y, and z? For each possible outcome, explain how we might arrive at those values. You will need to examine all possible interleavings of instructions.
7.7.2 [5] <7.3> How could you make the execution more deterministic so that only one set of values is possible?
Exercise 7.8
In a CCNUMA shared memory system, CPUs and physical memory are divided across compute nodes. Each CPU has local caches. To maintain the coherency of memory, we can add status bits into each cache block, or we can introduce dedicated memory directories. Using directories, each node provides a dedicated hardware table for managing the status of every block of memory that is “local” to that node. The size of each directory is a function of the size of the CCNUMA shared space (an entry is provided for each block of memory local to a node). If we store coherency information in the cache, we add this information to every cache in every system (i.e., the amount of storage space is a function of the number of cache lines available in all caches).
In the following proplems, assume that all nodes have the same number of CPUs and the same amount memory (i.e., CPUs and memory are evenly divided between the nodes of the CCNUMA machine).
7.8.1 [15] <7.3> If we have P CPU in the system, with T nodes in the CCNUMA system, with each CPU having C memory blocks stored in it, and we maintain a byte of coherency information in each cache line, provide an equation that expresses the amount of memory that will be present in the caches in a single node of the system to maintain coherency. Do not include the actual data storage space consumed in this equation, only account for space used to store coherency information.
7.8.2 [15] <7.3>If each directory entry maintains a byte of information for each CPU, if our CCNUMA system has S memory blocks, and the system has T nodes, provide an equation that expresses the amount of memory that will be present in each directory.
Exercise 7.9
Considering the CCNUMA system described in the Exercise 7.8, assume that the system has 4 nodes, each with a singlecore CPU (each CPU has its own L1 data cache and L2 data cache). The L1 data cache is storethrough, though the L2 data cache is writeback. Assume that system has a workload where one CPU writes to an address, and the other CPUs all read that data that is written. Also assume that the address written to is initially only in memory and not in any local cache. Also, after the write, assume that the updated block is only present in the L1 cache of the core performing the write.
7.9.1 [10] <7.3> For a system that maintains coherency using cachebased block status, describe the internode traffic that will be generated as each of the 4 cores writes to a unique address, after which each address written to is read from by each of the remaining 3 cores.
7.9.2 [10] <7.3> For a directorybased coherency mechanism, describe the internode traffic generated when executing the same code pattern.
7.9.3 [20] <7.3> Repeat 7.9.1 and 7.9.2 assuming that each CPU is now a multicore CPU, with 4 cores per CPU, each maintaining an L1 data cache, but provided with a shared L2 data cache across the 4 cores. Each core will perform the write, followed by reads by each of the 15 other cores.
7.9.4 [10] <7.3> Consider the system described in 7.9.3, now assuming that each core writes to byte stored in the same cache block. How does this impact bus traffic? Explain.
Exercise 7.10
On a CCNUMA system, the cost of accessing nonlocal memory can limit our ability to utilize multiprocessing effectively. The following table shows the costs associated with access data in local memory versus nonlocal memory and the locality of our application expresses as the proportion of access that are local.

Answer the following questions. Assume that memory accesses are evenly distributed through the application. Also, assume that only a single memory operation can be active during any cycle. State all assumptions about the ordering of local versus nonlocal memory operations.
7.10.1 [10] <7.3> If on average we need to access memory once every 75 cycles, what is impact on our application?
7.10.2 [10] <7.3> If on average we need to access memory once every 50 cycles, what is impact on our application?
7.10.3 [10] <7.3> If on average we need to access memory once every 100 cycles, what is impact on our application?
Exercise 7.11
The dining philosopher’s problem is a classic problem of synchronization and concurrency. The general problem is stated as philosophers sitting at a round table doing one of two things: eating or thinking. When they are eating, they are not thinking, and when they are thinking, they are not eating. There is a bowl of pasta in the center. A fork is placed in between each philosopher. The result is that each philosopher has one fork to her left and one fork to her right. Given the nature of eating pasta, the philosopher needs two forks to eat, and can only use the forks on her immediate left and right. The philosophers do not speak to one another.
7.11.1 [10] <7.4> Describe the scenario where none of philosophers ever eats (i.e., starvation). What is the sequence of events that happen that lead up to this problem?
7.11.2 [10] <7.4> Describe how we can solve this problem by introducing the concept of a priority? But can we guarantee that we will treat all the philosophers fairly? Explain.
Now assume we hire a waiter who is in charge of assigning forks to philosophers. Nobody can pick up a fork until the waiter says they can. The waiter has global knowledge of all forks. Further, if we impose the policy that philosophers will always request to pick up their left fork before requesting to pick up their right fork, then we can guarantee to avoid deadlock.
7.11.3 [10] <7.4> We can implement requests to the waiter as either a queue of requests or as a periodic retry of a request. With a queue, requests are handled in the order they are received. The problem with using the queue is that we may not always be able to service the philosopher whose request is at the head of the queue (due to the unavailability of resources). Describe a scenario with 5 philosophers where a queue is provided, but service is not granted even though there are forks available for another philosopher (whose request is deeper in the queue) to eat.
7.11.4 [10] <7.4> If we implement requests to the waiter by periodically repeating our request until the resources become available, will this solve the problem described in 7.11.3? Explain.
Exercise 7.12
Consider the following three CPU organizations: CPU SS: A 2core superscalar microprocessor that provides outoforder issue capabilities on 2 function units (FUs). Only a single thread can run on each core at a time. CPU MT: A finegrained multithreaded processor that allows instructions from 2 threads to be run concurrently (i.e., there are two functional units), though only instructions from a single thread can be issued on any cycle. CPU SMT: An SMT processor that allows instructions from 2 threads to be run concurrently (i.e., there are two functional units), and instructions from either or both threads can be issued to run on any cycle. Assume we have two threads X and Y to run on these CPUs that include the following operations:
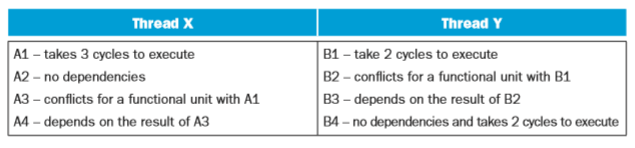
Assume all instructions take a single cycle to execute unless noted otherwise or they encounter a hazard.
7.12.1 [10] <7.5> Assume that you have 1 SS CPU. How many cycles will it take to execute these two threads? How many issue slots are wasted due to hazards?
7.12.2 [10] <7.5> Now assume you have 2 SS CPUs. How many cycles will it take to execute these two threads? How many issue slots are wasted due to hazards?
7.12.3 [10] <7.5> Assume that you have 1 MT CPU. How many cycles will it take to execute these two threads? How many issue slots are wasted due to hazards?
Exercise 7.13
Virtualization software is being aggressively deployed to reduce the costs of managing today’s high performance servers. Companies like VMWare, Microsoft and IBM have all developed a range of virtualization products. The general concept, described in Chapter 5, is that a hypervisor layer can be introduced between the hardware and the operating system to allow multiple operating systems to share the same physical hardware. The hypervisor layer is then responsible for allocating CPU and memory resources, as well as handling services typically handled by the operating system (e.g., I/O). Virtualization provides an abstract view of the underlying hardware to the hosted operating system and application software. This will require us to rethink how multicore and multiprocessor systems will be designed in the future to support the sharing of CPUs and memories by a number of operating systems concurrently.
7.13.1 [30] <7.5> Select two hypervisors on the market today, and compare and contrast how they virtualize and manage the underlying hardware (CPUs and memory).
7.13.2 [15] <7.5> Discuss what changes may be necessary in future multicore CPU platforms in order to better match the resource demands placed on these systems. For instance, can multithreading play an effective role in alleviating the competition for computing resources?
Exercise 7.14
We would like to execute the loop below as efficiently as possible. We have two different machines, a MIMD machine and a SIMD machine.
for (i=0; i < 2000; i++)
for (j=0; j<3000; j++)
X_array[i][j] = Y_array[j][i] + 200;
7.14.1 [10] <7.6> For a 4 CPU MIMD machine, show the sequence of MIPS instructions that you would execute on each CPU. What is the speedup for this MIMD machine?
7.14.2 [20] <7.6> For an 8wide SIMD machine (i.e., 8 parallel SIMD functional units), write an assembly program in using your own SIMD extensions to MIPS to execute the loop. Compare the number of instructions executed on the SIMD machine to the MIMD machine.
Exercise 7.15
A systolic array is an example of an MISD machine. A systolic array is a pipeline network or “wavefront” of data processing elements. Each of these elements does not need a program counter since execution is triggered by the arrival of data. Clocked systolic arrays compute in “lockstep” with each processor undertaking alternate compute and communication phases.
7.15.1 [10] <7.6> Consider proposed implementations of a systolic array (you can find these in on the Internet or in technical publications). Then attempt to program the loop provided in Exercise 7.14 using this MISD model. Discuss any difficulties you encounter.
7.15.2 [10] <7.6> Discuss the similarities and differences between an MISD and SIMD machine. Answer this question in terms of datalevel parallelism.
Exercise 7.16
Assume we want to execute the DAXP loop show on page 651 in MIPS assembly on the NVIDIA 8800 GTX GPU described in this Chapter. In this problem, we will assume that all math operations are performed on singleprecision floatingpoint numbers (we will rename the loop SAXP). Assume that instructions take the following number of cycles to execute.

7.16.1 [20] <7.7> Describe how you will constructs warps for the SAXP loop to exploit the 8 cores provided in a single multiprocessor.
Exercise 7.17
Download the CUDA Toolkit and SDK from http://www.nvidia.com/object/cuda_ get.html. Make sure to use the “emurelease” (Emulation Mode) version of the code (you will not need actual NVIDIA hardware for this assignment). Build the example programs provided in the SDK, and confirm that they run on the emulator.
7.17.1 [90] <7.7> Using the “template” SDK sample as a starting point, write a CUDA program to perform the following vector operations:
1) a - b (vectorvector subtraction) 2) a · b (vector dot product) The dot product of two vectors a = [a1, a2, … , an] and b = [b1, b2, … , bn] is defined as:

Submit code for each program that demonstrates each operation and verifies the correctness of the results.
7.17.2 [90] <7.7> If you have GPU hardware available, complete a performance analysis your program, examining the computation time for the GPU and a CPU version of your program for a range of vector sizes. Explain any results you see.
Exercise 7.18
AMD has recently announced that they will be integrating a graphics processing unit with their X86 cores in a single package, though with different clocks for each of the cores. This is an example of a heterogeneous multiprocessor system which we expect to see produced commericially in the near future. One of the key design points will be to allow for fast data communication between the CPU and the GPU. Presently communications must be performed between discrete CPU and GPU chips. But this is changing in AMDs Fusion architecture. Presently the plan is to use multiple (at least 16) PCI express channels for facilitate intercommunication. Intel is also jumping into this arena with their Larrabee chip. Intel is considering to use their QuickPath interconnect technology.
7.18.1 [25] <7.7> Compare the bandwidth and latency associated with these two interconnect technologies.
Exercise 7.19
Refer to Figure 7.7b that shows an ncube interconnect topology of order 3 that interconnects 8 nodes. One attractive feature of an ncube interconnection network topology is its ability to sustain broken links and still provide connectivity.
7.19.1 [10] <7.8> Develop an equation that computes how many links in the ncube (where n is the order of the cube) can fail and we can still guarantee an unbroken link will exist to connect any node in the ncube.
7.19.2 [10] <7.8> Compare the resiliency to failure of ncube to a fully connected interconnection network. Plot a comparison of reliability as a function of the added number of links for the two topologies.
Exercise 7.20
Benchmarking is field of study that involves identifying representative workloads to run on specific computing platforms in order to be able to objectively compare performance of one system to another. In this exercise we will compare two classes of benchmarks: the Whetstone CPU benchmark and the PARSEC Benchmark suite. Select one program from PARSEC. All programs should be freely available on the Internet. Consider running multiple copies of Whetstone versus running the PARSEC Benchmark on any of systems described in Section 7.11.
7.20.1 [60] <7.9> What is inherently different between these two classes of workload when run on these multicore systems?
7.20.2 [60] <7.9, 7.10> In terms of the Roofline Model, how dependent will the results you obtain when running these benchmarks be on the amount of sharing and synchronization present in the workload used?
Exercise 7.21
When performing computations on sparse matrices, latency in the memory hierarchy becomes much more of a factor. Sparse matrices lack the spatial locality in the data stream typically found in matrix operations. As a result, new matrix representations have been proposed. One the earliest sparse matrix representations is the Yale Sparse Matrix Format. It stores an initial sparse m×n matrix, M in row form using three onedimensional arrays. Let R be the number of nonzero entries in M. We construct an array A of length R that contains all nonzero entries of M (in lefttoright toptobottom order). We also construct a second array IA of length m + 1 (i.e., one entry per row, plus one). IA(i) contains the index in A of the first nonzero element of row i. Row i of the original matrix extends from A(IA(i)) to A(IA(i+1)–1). The third array, JA, contains the column index of each element of A, so it also is of length R.
7.21.1 [15] <7.9> Consider the sparse matrix X below and write C code that would store this code in Yale Sparse Matrix Format.
Row 1 [1, 2, 0, 0, 0, 0]
Row 2 [0, 0, 1, 1, 0, 0]
Row 3 [0, 0, 0, 0, 9, 0]
Row 4 [2, 0, 0, 0, 0, 2]
Row 5 [0, 0, 3, 3, 0, 7]
Row 6 [1, 3, 0, 0, 0, 1]
7.21.2 [10] <7.9> In terms of storage space, assuming that each element in matrix X is single precision floating point, compute the amount of storage used to store the Matrix above in Yale Sparse Matrix Format.
7.21.3 [15] <7.9> Perform matrix multiplication of Matrix X by Matrix Y shown below.
[2, 4, 1, 99, 7, 2]
Put this computation in a loop, and time its execution. Make sure to increase the number of times this loop is executed to get good resolution in your timing measurement. Compare the runtime of using a naïve representation of the matrix, and the Yale Sparse Matrix Format.
7.21.4 [15] <7.9> Can you find a more efficient sparse matrix representation (in terms of space and computational overhead)?
Exercise 7.22
In future systems, we expect to see heterogeneous computing platforms constructed out of heterogeneous CPUs. We have begun to see some appear in the embedded processing market in systems that contain both floating point DSPs and a microcontroller CPUs in a multichip module package. Assume that you have three classes of CPU: CPU A—A moderate speed multicore CPU (with a floating point unit) that can execute multiple instructions per cycle. CPU B—A fast singlecore integer CPU (i.e., no floating point unit) that can execute a single instruction per cycle. CPU C—A slow vector CPU (with floating point capability) that can execute multiple copies of the same instruction per cycle. Assume that our processors run at the following frequencies:

CPU A can execute 2 instructions per cycle, CPU B can execute 1 instruction per cycle, and CPU C can execute 8 instructions (though the same instruction) per cycle. Assume all operations can complete execution in a single cycle of latency without any hazards.
All three CPUs have the ability to perform integer arithmetic, though CPU B cannot perform floating point arithmetic. CPU A and B have an instruction set similar to a MIPS processor. CPU C can only perform floating point add and subtract operations, as well as memory loads and stores. Assume all CPUs have access to shared memory and that synchronization has zero cost. The task at hand is to compare two matrices X and Y that each contain 1024 × 1024 floating point elements. The output should be a count of the number indices where the value in X was larger or equal to the value in Y.
7.22.1 [10] <7.11> Describe how you would partition the problem on the 3 different CPUs to obtain the best performance.
7.22.2 [10] <7.11> What kind of instruction would you add to the vector CPU C to obtain better performance?
Exercise 7.23
Assume a quadcore computer system can process database queries at a steady state rate of requests per second. Also assume that each transaction takes, on average, a fixed amount of time to process. The following table shows pairs of transaction latency and processing rate.

For each of the pairs in the table, answer the following questions: 7.23.1 [10] <7.11> On average, how many requests are being processed at any given instant?
7.23.2 [10] <7.11> If move to an 8core system, ideally, what will happen to the system throughput (i.e., how many queries/second will the computer process)?
7.22.3 [10] <7.11> Discuss why we rarely obtain this kind of speedup by simply increasing the number of cores